



Il faut bien se dire qu'il n'y avait pas sur les chantiers des cathédrales de calculatrice. Rien de plus simple de nos jours d'en avoir une valeur approchée (car φ est un réel pur). Dans la construcion d'un édifice où les principaux outils du géomètre sont une canne unité et une corde à 12 noeuds (permettant d'obtenir l'angle droit et quelques autres angles particuliers entre autre), il faut être capable de tracer des longueurs valant un multiple de la canne unité, mais aussi de diviser cette unité, voir de prendre une valeur représentant une racine carré. Pour tous ces problèmes, il existe des techniques géométriques pures et surtout exactes, c'est à dire dont le résultat est le nombre recherché, et pas une approximation.
Le nombre d'or faisant intervenir une division par 2 et une racine carré, une construction spécifique et simple est trouvée. Ce n'est pas la seule. Il existait des situations où on variait de tracé. En voici une.
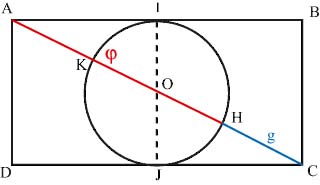
On trace tout d'abord un rectangle bicarré (2 x 1, c'est à dire un rectangle dont la longueur est le double de la largeur), et sa diagonale. Au centre du rectangle, on trace un cercle de diamètre 1/2.
La diagonale coupe le cercle en deux points K et H. On aura : φ = AH et g = CH
C'est tout !